Напомним, что плоскости называются перпендикулярными, если угол между ними прямой. А угол этот определяется так. Берут точку О на прямой С, по которой пересекаются плоскости , и проводят через нее в плоскостях прямые (рис. 1.9а). Углом между а и b и измеряется угол между . Когда этот угол прямой, то говорят, что плоскости взаимно перпендикулярны и пишут
Вы, конечно, уже заметили, что когда , то из трех прямых а, b, с любые две взаимно перпендикулярны (рис. 2.28). В частности, . Поэтому (по признаку перпендикулярности прямой и плоскости). Аналогично,
Итак, каждая из двух взаимно перпендикулярных плоскостей содержит перпендикуляр к другой плоскости. Более того, эти перпендикуляры заполняют взаимно перпендикулярные плоскости. (рис. 2.29).
Докажем последнее утверждение. Действительно, если через любую точку плоскости а провести прямую


То (по теореме 5 о параллельности перпендикуляров).
А для признака перпендикулярности плоскостей достаточно одного перпендикуляра к плоскости.
Теорема 7. (признак перпендикулярности плоскостей). Если плоскость проходит через перпендикуляр к другой плоскости, то эти плоскости взаимно перпендикулярны.
Пусть плоскость а содержит прямую а, перпендикулярную плоскости Р (рис. 2.28). Тогда прямая а пересекает плоскость Р в точке О. Точка О лежит на прямой С, по которой пересекаются . Проведем в плоскости Р через точку О прямую . Так как и b лежит в плоскости Р, то Следовательно,
Данный признак имеет простой практический смысл: плоскость двери, навешенной на перпендикулярный полу косяк, перпендикулярна плоскости пола при любых положениях двери (рис. 2.1). Другое практическое применение этого признака: когда требуется проверить, вертикально ли установлена плоская поверхность (стена, забор и т. п.), то это делают с помощью отвеса - веревки с грузом. Отвес всегда направлен вертикально, и стена стоит вертикально, если в любом ее месте отвес, располагаясь вдоль нее, не отклоняется.
При решении задач, в которых встречаются перпендикулярные плоскости, часто используются следующие три предложения.
Предложение 1. Прямая, лежащая в одной из двух взаимно перпендикулярных плоскостей и перпендикулярная их общей прямой, перпендикулярна другой плоскости.
Пусть плоскости взаимно перпендикулярны и пересекаются по прямой С. Пусть, далее, прямая а лежит в плоскости а и (рис. 2.28). Прямая а пересекает прямую С в некоторой точке О. Проведем через точку О в плоскости Р прямую b, перпендикулярную прямой с. Так как то . Поскольку , то (по теореме 2).
Второе предложение обратно первому.
Предложение 2. Прямая, имеющая общую точку с одной из двух взаимно перпендикулярных плоскостей и перпендикулярная другой плоскости, лежит в первой из них.

Пусть плоскости взаимно перпендикулярны, прямая а также прямая а имеет с плоскостью а общую точку А (рис. 2.30). Через точку А в плоскости а проведем прямую перпендикулярную прямой С - линии пересечения плоскостей . Согласно предложению Поскольку в пространстве через каждую точку проходит лишь одна прямая, перпендикулярная данной плоскости, то прямые а и совпадают. Так как лежит в плоскости а, то и а лежит в плоскости
Предложение 3. Если две плоскости, перпендикулярные третьей плоскости, пересекаются, то прямая их пересечения перпендикулярна третьей плоскости.

Пусть две плоскости , пересекающиеся по прямой а, перпендикулярны плоскости у (рис. 2.31). Тогда через любую точку прямой а проведем прямую, перпендикулярную плоскости у. Согласно предложению 2, эта прямая лежит и в плоскости а, и в плоскости Р, т. е. совпадает с прямой а. Итак,
Две плоскости, которые пересекаются, называются перпендикулярными , если третья плоскость, перпендикулярная прямой пересечения этих двух плоскостей, пересекает их по перпендикулярным прямым (см. рисунок).Любая плоскость, перпендикулярная к прямой пересечения перпендикулярных плоскостей, пересекает их по перпендикулярным прямым.
Признак перпендикулярности плоскостей
Теорема 1. Если плоскость проходит через прямую, перпендикулярную к другой плоскости, то эти плоскости перпендикулярны (см. рисунок).
Теорема 2. Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна линии их пересечения, то она перпендикулярна и ко второй плоскости (см. рисунок).
Пример применения теоремы 2
Пусть есть две перпендикулярные плоскости и , которые пересекаются по прямой a (см. рисунок). Найти расстояние от точки A , которая лежит в плоскости и не лежит в плоскости , плоскости .
В плоскости строим перпендикуляр к a через точку A . Пусть он пересекает a в точке B . AB - искомое расстояние.
Обратите внимание на такое.
1. Через точку вне плоскости можно провести множество плоскостей, перпендикулярных к этой плоскости (см. рисунок). (Но все они пройдут через перпендикулярную к этой плоскости прямую, которая проходит через данную точку.)

2. Если плоскость перпендикулярна к данной плоскости, то это не значит, что она перпендикулярна и к произвольной прямой, параллельной этой плоскости.
Например, на рисунке ниже , и пересекаются по прямой b , причем a входит в одной из плоскостей и . Следовательно, прямая a в то же время параллельная двум перпендикулярным плоскостям.

Определение. Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, и не принадлежащими одной плоскости.
Определение. Градусной мерой двугранного угла называется градусная мера любого из его линейных углов.
Определение. Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90 o .
Признак перпендикулярности двух плоскостей.
Свойства.
- В прямоугольном параллелепипеде все шесть граней представляют собой прямоугольники.
- Все двугранные углы прямоугольного параллелепипеда являются прямыми
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Задачи и тесты по теме "Тема 7. "Двугранный угол. Перпендикулярность плоскостей"."
- Двугранный угол. Перпендикулярность плоскостей
- Перпендикулярность прямой и плоскости - Перпендикулярность прямых и плоскостей 10 класс
Уроков: 1 Заданий: 10 Тестов: 1
- Перпендикуляр и наклонные. Угол между прямой и плоскостью - Перпендикулярность прямых и плоскостей 10 класс
Уроков: 2 Заданий: 10 Тестов: 1
- Параллельность плоскостей - Параллельность прямых и плоскостей 10 класс
Уроков: 1 Заданий: 8 Тестов: 1
- Перпендикулярные прямые - Начальные геометрические сведения 7 класс
Уроков: 1 Заданий: 17 Тестов: 1
Материал темы обобщает и систематизирует известные Вам из планиметрии сведения о перпендикулярности прямых. Изучение теорем о взаимосвязи параллельности и перпендикулярности прямых и плоскостей в пространстве, а также материал о перпендикуляре и наклонных целесообразно сочетать с систематическим повторением соответствующего материала из планиметрии.
Решения практически всех задач на вычисление сводятся к применению теоремы Пифагора и следствий из нее. Во многих задачах возможность применения теоремы Пифагора или следствий из нее обосновывается теоремой о трех перпендикулярах или свойствами параллельности и перпендикулярности плоскостей.
Понятие перпендикулярных плоскостей
При пересечении двух плоскостей у нас получается $4$ двугранных угла. Два угла равны $\varphi $, а два другие равны ${180}^0-\varphi $.
Определение 1
Углом между плоскостями называется минимальный из двугранных углов, образованных этими плоскостями.
Определение 2
Две пересекающиеся плоскости называются перпендикулярными, если угол между этими плоскостями равен $90^\circ$ (рис. 1).
Рисунок 1. Перпендикулярные плоскости
Признак перпендикулярности двух плоскостей
Теорема 1
Если прямая плоскости перпендикулярна другой плоскости, то эти плоскости перпендикулярны друг другу.
Доказательство.
Пусть нам даны плоскости $\alpha $ и $\beta $, которые пересекаются по прямой $AC$. Пусть прямая $AB$, лежащая в плоскости $\alpha $ перпендикулярна плоскости $\beta $ (рис. 2).

Рисунок 2.
Так как прямая $AB$ перпендикулярна плоскости $\beta $, то она перпендикулярна и прямой $AC$. Проведем дополнительно прямую $AD$ в плоскости $\beta $, перпендикулярно прямой $AC$.
Получаем, что угол $BAD$ - линейный угол двугранного угла, равный $90^\circ$. То есть, по определению 1, угол между плоскостями равен $90^\circ$, значит, данные плоскости перпендикулярны.
Теорема доказана.
Из этой теоремы следует следующая теорема.
Теорема 2
Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.
Доказательство.
Пусть нам даны две плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Плоскость $\gamma $ перпендикулярна прямой $c$ (рис. 3)

Рисунок 3.
Так как прямая $c$ принадлежит плоскости $\alpha $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\alpha $ и $\gamma $ перпендикулярны.
Так как прямая $c$ принадлежит плоскости $\beta $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\beta $ и $\gamma $ перпендикулярны.
Теорема доказана.
Для каждой из этих теорем справедливы и обратные утверждения.
Примеры задач
Пример 1
Пусть нам дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Найти все пары перпендикулярных плоскостей (рис. 5).
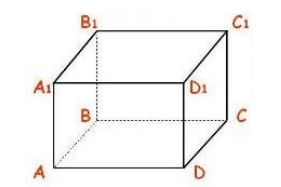
Рисунок 4.
Решение.
По определению прямоугольного параллелепипеда и перпендикулярных плоскостей видим следующие восемь пар перпендикулярных между собой плоскостей: $(ABB_1)$ и $(ADD_1)$, $(ABB_1)$ и $(A_1B_1C_1)$, $(ABB_1)$ и $(BCC_1)$, $(ABB_1)$ и $(ABC)$, $(DCC_1)$ и $(ADD_1)$, $(DCC_1)$ и $(A_1B_1C_1)$, $(DCC_1)$ и $(BCC_1)$, $(DCC_1)$ и $(ABC)$.
Пример 2
Пусть нам даны две взаимно перпендикулярные плоскости. Из точки одной плоскости проведен перпендикуляр к другой плоскости. Доказать, что эта прямая лежит в данной плоскости.
Доказательство.
Пусть нам даны перпендикулярные плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Из точки $A$ плоскости $\beta $ проведен перпендикуляр $AC$ к плоскости $\alpha $. Предположим, что $AC$ не лежит в плоскости $\beta $ (рис. 6).

Рисунок 5.
Рассмотрим треугольник $ABC$. Он является прямоугольным с прямым углом $ACB$. Следовательно, $\angle ABC\ne {90}^0$.
Но, с другой стороны, $\angle ABC$ является линейным углом двугранного угла, образованного этими плоскостями. То есть двугранный угол, образованный этими плоскостями не равняется 90 градусам. Получаем, что угол между плоскостями не равен $90^\circ$. Противоречие. Следовательно, $AC$ лежит в плоскости $\beta $.
Данный урок поможет желающим получить представление о теме «Признак перпендикулярности двух плоскостей». В начале него мы повторим определение двугранного и линейного угла. Затем рассмотрим, какие плоскости называются перпендикулярными, и докажем признак перпендикулярности двух плоскостей.
Тема: Перпендикулярность прямых и плоскостей
Урок: Признак перпендикулярности двух плоскостей
Определение. Двугранным углом называется фигура, образованная двумя полуплоскостями, не принадлежащими одной плоскости, и их общей прямой а (а - ребро).
Рис. 1
Рассмотрим две полуплоскости α и β (рис. 1). Их общая граница - l. Указанная фигура называется двугранным углом. Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.
Двугранный угол измеряется своим линейным углом. На общем ребре l двугранного угла выберем произвольную точку. В полуплоскостях α и β из этой точки проведем перпендикуляры a и b к прямой l и получим линейный угол двугранного угла.
Прямые a и b образуют четыре угла, равных φ, 180° - φ, φ, 180° - φ. Напомним, углом между прямыми называется наименьший из этих углов.
Определение. Углом между плоскостями называется наименьший из двугранных углов, образованных этими плоскостями. φ - угол между плоскостями α и β, если
Определение. Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°.

Рис. 2
На ребре l выбрана произвольная точка М (рис. 2). Проведем две перпендикулярные прямые МА = а и МВ = b к ребру l в плоскости α и в плоскости β соответственно. Получили угол АМВ. Угол АМВ - это линейный угол двугранного угла. Если угол АМВ равен 90°, то плоскости α и β называются перпендикулярными.
Прямая b перпендикулярна прямой l по построению. Прямая b перпендикулярна прямой а, так как угол между плоскостями α и β равен 90°. Получаем, что прямая b перпендикулярна двум пересекающимся прямым а и l из плоскости α. Значит, прямая b перпендикулярна плоскости α.
Аналогично можно доказать, что прямая а перпендикулярна плоскости β. Прямая а перпендикулярна прямой l по построению. Прямая а перпендикулярна прямой b, так как угол между плоскостями α и β равен 90°. Получаем, что прямая а перпендикулярна двум пересекающимся прямым b и l из плоскости β. Значит, прямая а перпендикулярна плоскости β.
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Доказать:

Рис. 3
Доказательство:
Пусть плоскости α и β пересекаются по прямой АС (рис. 3). Чтобы доказать, что плоскости взаимно перпендикулярны, нужно построить линейный угол между ними и показать, что этот угол равен 90°.
Прямая АВ перпендикулярна по условию плоскости β, а значит, и прямой АС, лежащей в плоскости β.
Проведем прямую АD перпендикулярно прямой АС в плоскости β. Тогда ВАD -линейный угол двугранного угла.
Прямая АВ перпендикулярна плоскости β, а значит, и прямой АD, лежащей в плоскости β. Значит, линейный угол ВАD равен 90°. Значит, плоскости α и β перпендикулярны, что и требовалось доказать.
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей (рис. 4).
Доказать:

Рис. 4
Доказательство:
Прямая l перпендикулярна плоскости γ, а плоскость α проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости α и γ перпендикулярны.
Прямая l перпендикулярна плоскости γ, а плоскость β проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости β и γ перпендикулярны.



